1.4 Numeri complessi

L'unita' immaginaria  e' rappresentata da I  (si tratta di un alias per 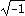). L'aritmetica e' automatica:

>

z:=3+4*I;

Parte reale di z:

>

Re(z);

Parte immaginaria di z;

>

Im(z);

Forma polare di z:

>	convert(z,polar);

Calcolo di arctan(4/3); il risultato viene dato in radianti, e occorre chiedere la forma decimale:

>	evalf(arctan(4/3);

Per attivare quanto Maple conosce dei numeri complessi e' utile il programma evalc (evaluate usando l'aritmetica dei numeri complessi).

>	evalc(1/a);

>	b:=2+p-q*I;

>

b1:=1/b;

>	evalc(b1);

>	b2:=abs(b1);

>	evalc(b2);

>	a:=evalf(arctan(4/3),15);

Trasformiamo in gradi, ricordando che 1rad=180/Pi gradi, dove Pi significa "p greco".

>

Pi;

Calcoliamo p greco, ad esempio con 10 cifre decimali, e 1 radiante con questo valore di p greco:

>	p:=evalf(Pi,10);

>	rad:=180/p;

Con questo valore di rad calcoliamo a=arctan(4/3) in gradi:

>

a*%;

Per ottenere i primi moltiplichiamo la parte dopo la virgola per 60:

>	0.13010234*60;

Per ottenere i secondi moltiplichiamo la parte dopo la virgola per 60:

>	0.80614040*60;

L'angolo è quindi di 53 gradi, 7 primi, 48 secondi,...