3.3 Alberi e tipi

Le operazioni che Maple effettua sono manipolazioni di alberi di espressioni. Tutti gli oggetti Maple sono alberi con una radice, e quest'ultima determina il tipo di base dell'espressione, tipo che si ottiene con il comando whattype. I nodi dell'albero corrispondono alle operazioni e ai simboli di funzioni, le foglie agli interi e ai simboli che rappresentano dei numeri. La divisione (sottrazione) corrisponde a una moltiplicazione per l'inverso (addizione dell'opposto).

Si definisce tipo (type) una classe di espressioni che hanno delle proprieta' in comune (es: integer, numeric, algebraic, function, procedure,..)

>	type(sin(x),integer);

>	type(1/2,integer);

>	type(1234,integer;

>	?function;

>	type(sin(x),function);

>	type(sin(x),procedure);

>	type(sin,function);

>	type(sin,procedure);

Si osservi la distinzione tra un'espressione di tipo procedure e una di tipo function, (che sarebbe meglio definire function call). In Maple e' il tipo procedure, e non il tipo function, che corrisponde alla nostra idea di funzione matematica. Dunque:

             f(x)= function call (o function application) e f = procedure.    

>	whattype(sin(x));

>	whattype(a+b);

>	whattype(x^2);

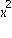e' di tipo "esponenziazione"

>	whattype ((x-2)*(x+2)+4);

tipo "somma"

>	f:=exp(3)*cos(x*y*w+Pi/3)*(x^2-y+4/3);

>	whattype(f);

tipo "prodotto"

>	type(x+y,'polynom')

>

a,b,5;

>	whattype(%);

Si possono creare nuovi tipi:

>	nuovotipo:=name^integer;

>	type(x^4,nuovotipo);

>	type(exp(1)^3,nuovotipo);

>	type(3^4,nuovotipo);

falso perche' "3" non e' un nome. Un nome non puo' cominciare con una cifra: un nome e' dato da una lettera seguita da lettere, cifre,trattini,ecc.

Vi sono essenzialmente tre operazioni di base sugli alberi delle espressioni:

-- analizzare gli alberi;

-- determinarne le componenti;

-- modificarli.

Analisi di un albero. L'abbiamo appena vista

Determinazione delle componenti di un albero. Se T e' l'albero Maple che rappresenta un'espressione espr, gli operandi di expr sono le expr rappresentate dai sottoalberi. Ricordiamo che la successione degli operandi viene richiamata con op(expr), e il loro numero con nops(expr):

>	f:=exp(3)*cos(x*y*w+Pi/3)*(x^2-y+4/3);

>

op(f);

>

nops(f);

>	op(2,f); # qual e' il secondo operando dell'expr f?

>	op(1..2,f); # quali sono il primo e il secondo operando di f?

>	op(1,op(2,f)); # qual e' il primo operando del secondo operando di f?

>	op(0,f); # rimanda alla radice dell'albero (eccetto nel caso di funzioni o di tavole e serie)

Modifica di un albero. Si fa con le istruzioni convert,subsop,subs, ecc. Queste istruzioni modificano l'albero nel senso che creano una copia modificata dell'argomento su cui le istruzioni operano. Se T e' l'albero che rappresenta espr :

convert(espr,f) crea una copia di T nella quale solo la radice e' sostituita da una nuova radice determinata da f;

subsop(i=f,espr) crea una copia di T nella quale l'i-esimo operando e' sostituito dall'espressione f. Sono possibili piu' sostituzioni;

subs(x=f, espr) crea una copia di T nella quale ogni sottoalbero corrispondente all'espressione x  e' sostituito dall'albero che rappresenta f.

>	subsop(2=-3/2,f);

>	subs(x=2,f);

L'espressione ottenuta sostituendo un'espressione g a f puo' ancora contenere delle occorrenze di g quando queste non corrispondono a una sottoespressione di f :

>	subs(x*y=3,f);

non e' cambiato niente perche' x*y non e' un'espressione di f :

>	has(f,x*y);

>	h:=x*y+5-4*x*y*w+2*x-y+y*w;

>	subs(x*y=1,h);

>	subs(y*w=1,h);

>	subs(x*w=1,h);

subs non rivaluta completamente l'espressione ottenuta per sostituzione; e' quanto succede qui:

>	g:=subs(x*y*w=2/3*Pi,f):

>

g;

Le semplificazioni abituali sui numeri e le costanti vengono pero' effettuate:

>	q:=2*x*y*(y+I/2)-4*I+3;

>	subs(y=I/2,q);

Infine, se si vogliono sostituire piu' sottoespressioni in una espressione vi sono due casi:

i) le sostituzioni avvengono una dopo l'altra:

>	subs(x=y,y=x,f);

ii) le sostituzioni avvengono simultaneamente se si raggruppano in un insieme (o una lista), che diventa un paramentro della funzione subs :

>	subs({x=y,y=x},f);