6.1 LinearAlgebra

Il package LinearAlgebra contiene numerose routines che permettono di definire matrici, vettori, ecc. e di operare con questi oggetti.

In una sessione Maple, o in una sua parte che richiede questo package, occorre dichiarare:

> with(LinearAlgebra):

Matrici. Una matrice si può definire in più modi:

Mediante la lista delle righe:

> M:=Matrix([[1,2,3],[4,5,6]]);

Definendo una funzione del posto (i,j):

> f:=(i,j)->1/(i+j-1);

e quindi specificando le dimensioni della matrice:

> Matrix(2,3,f);

La matrice definita dalla f di sopra si chiama matrice di Hilbert. Esiste anche un comando che la fornisce direttamente:

> H:=HilbertMatrix(3,4):

> H1:=HilbertMatrix(4);

Per estrarre l'elemento che sta nel posto (i,j) di una matrice M basta chiedere M[i,j]:

> H1[2,3];

Determinanti: Determinant(M)

> for i to 6 do Determinant(HilbertMatrix(i)) od:

>

> f1:=(i,j)->evalf(1/(i+j-1));

> H2:=Matrix(4,f1):

> for i to 6 do Determinant(Matrix(i,f1)) od:

>

Matrici diagonali. Gli elementi della diagonale vanno dati sotto forma di vettore: DiagonalMatrix(V,m,n), m numero di righe, n di colonne

> V:=<a,b,c,d>:

> DiagonalMatrix(V,5,6):

Matrice identica: IdentityMatrix(m,n), IdentityMatrix(n), matrice identica mxn o nxn

> IdentityMatrix(4,5); IdentityMatrix(4);

Matrice nulla: ZeroMatrix(m,n), ZeroMatrix(n)

> ZeroMatrix(4,5);  ZeroMatrix(4);

Matrice simmetrica

Si inizializza con la matrice nulla:

> M:=Matrix(n,shape=symmetric);  # dà la matrice nulla n x n

> M:=Matrix(3,shape=symmetric);

Si assegnano valori M[i,j], e si ottiene la matrice che ha M[i,j]=M[j,i]:

> M[1,2]:=-1;

> M;

e così per gli altri elementi.

Matrice triangolare

Come per la matrice simmetrica, si inizializza con la matrice nulla. Vi sono due opzioni triangular (che equivale a triangular[upper]) e triangular[lower].

> M:=Matrix(n,shape=triangular), ovvero M:=Matrix(n,shape=triangular[lower]),  # si crea la matrice nulla n x n e si stabilisce se la matrice sarà triangolare superiore o inferiore

> M:=Matrix(3,shape=triangular);

> M[1,2]:=1; M[1,3]:=-1;M[2,3]:=1/2;

> M;

Si può anche inizializzare con una matrice che ha tutti 1 sulla diagonale e 0 altrove:

> M:=Matrix(3,shape=triangular[lower,unit]):

> M[2,1]:=1; M[3,1]:=-1; M[3,2]:=1/2;

> M;

Trasposta di una matrice:

> Transpose(M):

Matrice di Vandermonde:

> VandermondeMatrix(V):

> T:=Transpose(%):

> h:=Determinant(T):

> h1:=factor(h): # si vede da qui che il determinante di Vandermonde è zero se e solo se due degli elementi a,b,... sono uguali.

Matrice inversa

> A:=HilbertMatrix(4);

> B:=MatrixInverse(A): # si osservi che l'inversa di una matrice di Hilbert è a elementi interi e a segni alterni su righe e colonne

Il prodotto di due matrici A e B si ottiene con il comando A.B. Verifichiamo che B è effettivamente l'inversa di A facendo il prodotto:

> A.B:

Potenza di una matrice: M^n oppure MatrixPower(M,n)

> A^2;

> MatrixPower(A,2);

Matrice di Sylvester di due polinomi

> f:=a1*x^2+a2*x+a3:

> g:=b1*x^3+b2*x^2+b3*x+b4:

> SylvesterMatrix(f,g,x):

Il determinante della matrice di Sylvester è il risultante dei due polinomi. Il risultante è zero se e solo se i due polinomi hanno una radice in comune.


Esempio. Due polinomi che hanno una radice in comune:

> f:=expand((x-1)*(x^3-x-1));

> g:=expand((x-1)*(x+1));

> SylvesterMatrix(f,g,x);

> Determinant(%);

> resultant(f,g,x);

Altro esempio:

> f:=x^4-x^3-2*x-1; g:=x^3+1;

> resultant(f,g,x);

I due polinomi non hanno radici comuni.

Estrazione di elementi e sottomatrici

> M[i,j]; # estrae l'elemento di posto (i,j) della matrice M

> f:=(i,j)->2*i-j:

> M1:=Matrix(5,f);

> M1[2,3];

M[i..j,h..k]: # estrae dalla matrice composta dalle righe comprese tra la i e la j (incluse) della matrice M la matrice composta dalle colonne della M comprese tra la h e la k (incluse)

> M1[1..4,2..3]; #matrice 4 x 2

> M1[3..5,4..5]; # matrice 3 x 2

> M1[1..1,2..4]; #matrice 1 x 3

> M1[3..3,3..5]; #matrice 1 x 3

> M1[3..3,2..2]; #matrice 1 x 1

> M1[3..5,-2..-1]; # estrae dalla matrice composta dalle righe comprese tra la 3 e la 5 della matrice M le colonne comprese tra la penultima e l'ultima. E' una matrice 3 x 2.

L'indice i sceglie la i-esima riga (colonna), -1 l'ultima, -2 la penultima, ecc.

> M1[3..4,1..-1]; # estrae dalla matrice composta dalle righe comprese tra la 3 e la 4 della matrice M le colonne comprese tra la prima e l'ultima (quindi equivale a M1[3..4,1..5]). E' una matrice 2 x 5.

Il comando Minor

> Minor(A,r,c); # determinante della matrice ottenuta sopprimendo la riga r e la colonna s da A, ed è equivalente a

> Minor(A, r, c, output=['determinant']);

Per avere la matrice:

> Minor(A, r, c, output=['matrix']); # crea la matrice ottenuta sopprimendo la riga r e la colonna s da A

> Minor(A, r, c, output=['matrix','determinant']);# dà insieme matrice e determinantea del minore

> A:=Matrix([[-16,-17,87,-108],[8,9,-42,54],[-3,-3,16,-18],[-1,-1,6,-8]]):

Eliminazione di Gauss

> GaussianElimination(A);

Polinomio caratteristico della matrice A

E' il determinante della matrice A-x*id, dove id è la matrice identica:

> A-x*IdentityMatrix(4);

> Determinant(A-x*IdentityMatrix(4));

Maple ha un comando che lo dà direttamente:

> c:=CharacteristicPolynomial(A,x);

Per il teorema di Hamilton Cayley si ha p(A)= 0 (matrice nulla). Verifica:

> subs(x=A,c);

> evalm(%);

Polinomio minimo della matrice A

E' il polinomio m(x) monico di grado minimo tale m(A)=0. Divide tutti i polinomi f(x) tali che f(A)=0.

Maple ha il comando:

> m:=MinimalPolynomial(A,x);

> rem(c,m,x); # il polinomio minimo divide in particolare il polinomio caratteristico

Autovalori

Sono le radici del polinomio caratteristico

> Eigenvalues(A); # si può chiedere la lista delle radici:

> Eigenvalues(A, output='list');

> solve(c,x);

Forma normale di Smith di una matrice intera o polinomiale

Una matrice si dice in forma normale di Smith se:

i) è diagonale;

ii) i polinomi e_1(x),e_2(x),...,e_n(x) (gli interi) sulla diagonale sono tali che ognuno è multiplo del precedente (dal secondo in poi). Gli e_i(x) sono i fattori invarianti della matrice; i polinomi della fattorizzazione degli e_i(x) in potenze di polinomi irriducibili (in potenze di primi) sono i divisori elementari della matrice);

iii) il coefficiente direttore degli e_i(x) è 1.

Ogni matrice si può portare a forma normale di Smith mediante trasformazioni elementari.

> SmithForm(A);

> SmithForm(A-x*IdentityMatrix(4));

> expand((x-1)*(2-3*x+x^3));

L'ultimo polinomio e_n(x) coincide con il polinomio minimo.

> factor(2-3*x+x^3);

La matrice A ha dunque tre divisori elementari (le cui radici sono gli autovalori della matrice):

> (x-1)^2,x-1,x+2;

e dunque ha tre blocchi di Jordan: un blocco 2 x 2, relativo alla radice doppia di 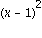(x-1)^2 , e due

blocchi 1 x 1 relativi alle radici di x-1 e x+2.

Blocchi di Jordan

Dato un numero a, un blocco di Jordan relativo ad a è una matrice ha tutti a sulla diagonale principale, tutti 1 sulla diagonale secondaria superiore e zero altrove.

Forma di Jordan

Una matrice di Jordan è una matrice diagonale costituita da blocchi di Jordan. La forma di Jordan di una matrice A è la matrice che ha sulla diagonale blocchi di Jordan relativi agli autovalori di A: vi sono tanti blocchi quanti sono i divisori elementari e_i(x) (diversi da 1), ciascuno di dimensione pari al grado di e_i(x).

Sul campo complesso, ogni matrice A si può portare in forma di Jordan: esiste cioè una matrice Q tale che 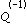Q^(-1) AQ =J.  

> J := JordanForm(A);

Il seguente comando fornisce sia J che Q:

> Q := JordanForm(A,output='Q');

> Q1:=MatrixInverse(Q);

> Q1.A.Q; # verifica

Prodotto di una matrice per un vettore

> u:=<1|0|-1|1>; # vettore riga

> u.A;

> v:=<1,0,-1,1>; # vettore colonna

> A.v;

Sistemi di equazioni lineari

> f:=2*x-y+3*z-1;

> g:=2*x-y+z+3;

> h:=x-4*y+2*z;

> solve({f,g,h},{x,y,z});

> M:=Matrix([[2,-1,3],[2,-1,1],[1,-4,2]]):

> Determinant(M);

> f:=x+2*y-3*z+4*u;

> g:=x+3*y-z;

> h:=6*x+z+2*u;

> solve({f,g,h},{x,y,z,u});

> M1:=Matrix([[1,2,-3,4],[1,3,-1,0],[6,0,1,2]]);

> ker:=NullSpace(M1);