Ocean currents are the most significant parameters for our study, significantly impacting the air-sea interaction, pollution and transport of ocean trace. We propose a global estimation of surface ocean currents from space by developing physical models and algorithm at the best spatial a temporal resolution. This is achieved by the inversion of the ocean heat conservation equation in upper ocean mixed layers applied to sea surface temperature satellite observation ad sea level altimeter measurements. The study evidenced that our synergistic approach can improve the present-day derivation of the surface currents up to 30% locally, allowing retrieval of both small scales and geostrophic features. In addition, by using Finite-Scale Lyapunov Exponents, the surface current fields produced have also been used for a rigorous, quantitative evaluation of satellite-based Lagrangian dispersion numerical trajectories.

Signals are used in our everyday life to send and receive information or to extract information from an unknown environment. Typically, signals are defined over a metric space, i.e. time and space. The goal of this talk is to present a set of tools to analyze signals that are defined over a topological (e.g., not necessarily metric) space, i.e. a set of points along with a set of neighbourhood relations for each point. Motivating applications span from gene regulatory networks to social networks, etc. We introduce the Graph Fourier Transform (GFT), derive an uncertainty principle for signals defined over graphs and set the basis for a sampling theory over graphs. We start from signals defined over graphs and then we move to the most general case of signals defined over simplicial complexes. Finally, we illustrate some applications to the recovery of the electromagnetic field from a subset of observations, the inference of the brain functional activity network from electrocorticography (ECoG) signals collected in an epilepsy study and theprediction of data traffic over telecommunication networks.

Stochastic individual base models, that is, measure valued Markov processes describing the evolution of interacting biological populations, have proven over the last years to be effective models in deriving key features of the theory of adaptive dynamics, such as the canonical equation of adaptive dynamics, the trait substitution sequence and the polymorphic evolution sequence. In this talk I review these models an the diverse emerging scaling limits, and I report on recent progress in applying such models to the modelling of cancer therapies, and in particular to immunotherapy and combination therapies of melanoma, based on experimental data by colleagues from the Bonn university hospital.

Euglena gracilis is a unicellular protist exhibiting different motility strategies: swimming by flagellar propulsion, or crawling thanks to large amplitude shape changes of the whole body (a behavior known as amoeboid motion, or metaboly).
Swimming is propelled by the non-planar beating of a composite flagellum powered by an axoneme, with molecular motors sliding over microtubule bundles (arranged according to the “standard” 9+2 architecture).
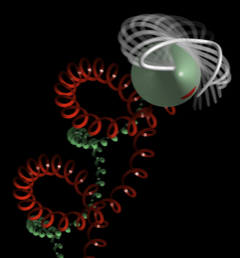The non-planar beating of the flagellum leads in turn to helical trajectories coupled with body rotations, and these rotations play an important role in the phototactic behavior of E. gracilis.
Confinement triggers a behavioral change, namely, E. gracilis switches from flagellar swimming to ameboid motion, which is propelled by peristaltic waves along the body of the organism. These are powered by molecular motors driving the relative sliding of pellicle strips lying underneath the plasma membrane. The mechanisms controlling the gait switch in this unicellular organism are still unknown.
Our most recent findings on the motility of E. gracilis, which are the result of a combined theoretical and experimental analysis, will be surveyed.

Image: flagellar shapes and resulting trajectories of the cell body (green) and eyespot (red) of Euglena gracilis

Cooperation can be sustained by institutions that punish free-riders. Such institutions, however, tend to be subverted by corruption if they are not closely watched. Monitoring can uphold a regime of honesty and cooperation, but usually comes at a price. The temptation to skip monitoring regularly leads to outbreaks of corruption and the breakdown of cooperation. We model the corresponding cycle by means of evolutionary game theory, using analytical methods and numerical simulations. The results confirm the view that transparency is a major factor in fighting corruption.

Granular materials are made of macroscopic particles, called grains: sand, rice, sugar and powders are typical examples. They are important in our everyday life, in many industrial applications and in the prevention of geophysical hazards. In physics, mainly in the realm of non-equilibrium statistical mechanics, granular systems are an inspiring source of phenomena and questions. The simplest model of granular material is a "fluid" made of inelastic hard spheres. For such a system - in the dilute limit - the classical program of kinetic theory (Boltzmann equation, Chapman-Enskog-based hydrodynamics, and much more) has been developed by physicists and mathematicians in the last decades. In this seminar, after recalling a few key results of such a theoretical activity, I will focus on a series of experiments made in my laboratory in the last 5 years. They concern the statistical properties of a massive probe immersed in a steady state granular fluid. The fluid is obtained by vibro-fluidization of a large number of hard spheres of different materials, while the probe is a rigid rotator whose angular displacement and angular velocity are the key observables. In the dilute limit one conjectures a Markovian approximation for the rotator's dynamics which explains many aspects of the experiment, including a qualitative understanding of "motor effects" in the presence of rotator's asymmetries. Further noticeable facts appear when the granular fluid is not dilute, mainly the violation of the mobility-diffusivity Einstein relation, and anomalous diffusion. For these phenomena a predictive theory is lacking and only phenomenological models are available.