10 novembre
ore 15:00
Sala di Consiglio |
Fabio Sciarrino
Quantum information processing via a photonics platform

Quantum computers exploit the incredible possibilities of quantum mechanics to significantly enhance computing power, compared with the computers currently available based on a conventional approach. In this context, it is essential to experimentally demonstrate the potential of quantum computers. Recently, the study of computational problems that produce samples from probability distributions has highlighted a path forward to demonstrate quantum advantage, corresponding to a scenario where a quantum device solves a specific computational problem faster than any classical system, as well as first applications. In particular we will discuss a computational problem that has been proposed as a candidate to obtain an unequivocal quantum computational advantage. The problem consists in sampling from the output distribution of indistinguishable bosons in a linear interferometer. There is strong evidence that such an experiment is hard to classically simulate, but it is naturally solved by dedicated photonic quantum hardware. This prospect has stimulated much effort resulting in the experimental implementation of progressively larger devices. We will review recent advances in photonic boson sampling, describing both the technological improvements achieved and the future challenges.
|
19 maggio
ore 12:00
Sala di Consiglio |
Christophe Pouzat
Neuronal network structure inference by simulation
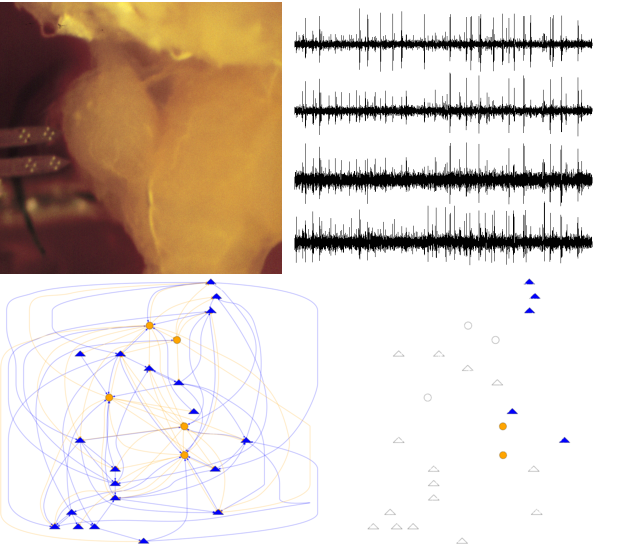
Neurophysiologists are nowadays able to record from a large number of extracellular
electrodes and to extract, from the raw data, the sequences of action potentials
or spikes generated by many neurons. Unfortunately these "many neurons" still
represent only a tiny fraction of the neuronal population which constitutes the network.
Using association statistics such as cross-correlograms, they try to infer the
structure of the network formed by the recorded neurons.
But this inference is compromised by the tremendous under-sampling of the neuronal
population and by the errors made during the sequences reconstruction. This yields
a "network picture" usually called a "functional network" whose features depend strongly
on the recording conditions (such as the presence/absence of a stimulation).
Considering that reconstructing the network formed by the recorded neurons is an
ill-posed problem, I propose to focus instead on the "generative probability distribution" of the network:
what is the probability to have a connection from a type A neuron to a type B neuron? Is the
probability to have a connection from neuron Y of type B to neuron X of type A dependent on the
presence of a connection from X to Y? To that end, the key idea is to simulate first the whole
network using a simplified neuronal dynamics and different (parametrized) generative probability
distributions. The association statistics obtained from the simulations and from the actual data
are then compared and the model parameters are tuned in order to improve the match. This type of
approach is now commonly used in several fields under different names like "Approximate Bayesian
Computation" or "Simulation based Inference". I will illustrate on a idealized case, inspired by the first olfactory relay of an insect, how the "over representation of reciprocal
connections" can be addressed.
|
31 Marzo
ore 12:00
Sala di Consiglio |
Simon Guest
Zero-stiffness structures

The talk will provide a compendium of ’zero-stiffness’ structures, describing three classes of structures that remain in a neutral state of equilibrium, even while they undergo large (and clearly geometrically nonlinear) displacements, with part or all of each structure undergoing large (but elastic) deformations. The structures will not be abstract theoretical constructions,
but real structures modelled using reasonable assumptions. Physical examples will be demonstrated.
|
24
Febbraio
ore 12:00
Aula Picone |
Mirko Degli Esposti
Entropy, Irreversibility, DNA sequences… and Fake Faces

Entropy and irreversibility, two fundamental concepts underlying physical processes, and now also at the core of digital processes for simulation and evolution of artificial models. We will touch on some of these aspects, taking as our starting point the well-defined and well-explored mathematical context of infinite sequence spaces over finite alphabets. As we will see, universal estimators of typical signal entropy and cross entropy, based on the asymptotics of recurrences and waiting times, play an important role in information theory, and we will discuss some mathematical results. Starting from their construction, we will introduce and discuss universal estimators of typical signals of entropy production in the context of nonequilibrium statistical mechanics of one-sided shifts on finite alphabets. Finally, we will discuss some applications to DNA sequences, particularly in understanding the so-called Second Chargaff Rule, a still unexplained family of empirical symmetries present in "most" genetic sequences. We will conclude with some suggestions to show how concepts proper to statistical mechanics and thermodynamics, such as entropy and irreversibility, have become fundamental even in the most recent synthetic image generation models.
In collaboration with Giampaolo Cristadoro Vojkan Jakšić, Renaud Raquépas.
|
27
Gennaio
ore 14.00
Sala di Consiglio |
Laura
Palagi
From black forests to interpretable
trees: an overview and recent development on
Optimal classification tree
In recent years there has been a growing
attention to machine learning models which are
able to give explanatory insights on the
decisions made by the algorithm. Thanks to their
interpretability, decision trees have been
intensively studied for classification tasks,
and, due to the remarkable advances in
Mixed-Integer Programming (MIP), various
approaches have been proposed to formulate the
Optimal Classification Tree (OCT) problem as a
MIP model starting from the seminal paper
[Bertsimas D. and J. Dunn. "Optimal
classification trees." Machine Learning 106.7
(2017)]. In this talk, we will make an overview
on classification trees and random forests and
on the optimal tree classification formulation.
First, we present a novel formulation for binary
classification using OCT and exploiting the
generalization capabilities of another well know
machine learning classifiers which are Support
Vector Machines [Cortes C. , and V. Vapnik.
"Support vector machine." Machine learning 20.3
(1995)]. In particular, the maximum MARGin
Optimal Classification Tree (MARGOT) uses at
each node of the decision tree a regularized
Linear SVM to define a linear classifiers with
maximum margin in a tree structure. The
resulting model is a Mixed Integer Quadratic
Programming problem. The model can also include
feature selection constraints which allows to
define a hierarchy on the subsets of features
which mostly affect the outcome. We further
present an OCT for approximating random forests
with a single tree following a similar modelling
approach. Numerical results on benchmark dataset
are reported.
Joint work with:
Giulia Di Teodoro, Marta Monaci,
Federico D'onofrio, Giorgio Grani
Immagine generata con piattaforma
DALL·E 2 (DALL·E 2 (openai.com))
usando la
descrizione in linguaggio naturale
"a decision tree painted by pietr
mondrian"
|
|
| | | | |